風向(wind direction)
風が吹いてくる方向。北、北北東、北東、東北東、東、東南東、南東、南南東、南、南南西、南西、西南西、西、西北西、北西、北北西に区分する場合は16方位風向と呼ぶ。東風の風向を90°、南風の風向を180°、西風の風向を270°、北風の風向を360°として、1°間隔または5°間隔、10°間隔で表す方法もある。風速が0.1ms-1未満の場合は、静穏と呼び、風向は決定できない。
|
フーリエ解析(Fourier
analysis)
フーリエ級数やフーリエ変換を用いて複数の基本的波の重ね合わせによって複雑な関数や信号を表現することをフーリエ解析と言う。調和解析とも呼ばれる。
|
フーリエ級数(Fourier
series)
ある一定周期Tをもつ時間関数f(t) は関数f(t)から定められるフーリエ係数を各項の係数とする三角級数に
∞
f(t)=a0/2+∑{ancos(nω0t)+bnsin(nω0t)}
n=1
と展開することができ、得られた三角級数は関数f(t)のフーリエ級数と呼ばれる。ここで、t;時間、n;波数、ω0;基本振動数(=2π/T)である。
この式は、一定周期Tをもつ変動は、時間平均値a0/2に、一周期Tに1回振動する波動、2回振動する波動、3回振動する波動、……、無限回振動する波動が重なったものとして表現できることを意味している。関数f(t)の一周期Tに1回振動する成分a1cos(ω0t)+b1sin(ω0t)を基本成分と呼び、n>1のancos(nω0t)+bnsin(nω0t)を第n次高調成分と呼ぶ。
上式は、
∞
f(t)=a0/2+∑(an2+bn2)0.5cos(nω0t+φn)
n=1
または、
∞
f(t)=a0/2+∑(an2+bn2)0.5sin(nω0t+ψn)
n=1
と変形でき、これらの表現も、同様に、関数f(t)のフーリエ級数と呼ばれ、(an2+bn2)0.5は第n次高調成分の振幅、φnとψnは初期位相と呼ばれる。
関数f(t)の値が、Δt間隔で離散的に一周期中に等間隔にN個得られている場合には、フーリエ係数は第N/2次高調成分までしか求めることができない。このため、本来は∞まで高次の高調成分を求める必要があるが、第N/2次高調成分までで打ち切った三角級数を有限フーリエ級数と呼ぶ。
フーリエ級数の定義式を
∞
f(t)-a0/2=∑(an2+bn2)0.5sin(nω0t+ψn)
n=1
と変形し、その自乗を時間t0~t0+Tの間積分すると、
t0+T
∞ ∞
t0+T
∫{f(t)-a0/2}2dt=∑∑{(am2+bm2)0.5(an2+bn2)0.5∫sin(mω0t+ψn)sin(nω0t+ψn)dt}
t0
m=1n=1
t0
となるが、三角級数の直交性から、
t0+T
∞
t0+T
∫{f(t)-a0/2}2dt=∑{(an2+bn2)∫sin2(nω0t+ψn)dt}
t0
n=1
t0
でなくてはならない。両辺の定積分が
t0+T
∫{f(t)-a0/2}2dt=2πσ2
t0
t0+T
∫sin2(nω0t+ψn)dt=π
t0
であるから、
∞
∑{(an2+bn2)=2σ2
n=1
でなくてはならない。ここで、(an2+bn2);振幅の自乗、σ2;分散である。つまり、関数f(t)のフーリエ級数の係数の自乗の総和は、関数f(t)の分散の2倍に等しくなる。このため、
(an2+bn2)/2
は第n次高調成分の説明度を意味している。
|
フーリエ係数(Fourier coefficient)
ある一定周期Tをもつ時間関数f(t) をフーリエ級数
∞
f(t)=a0/2+∑{ancos(nω0t)+bnsin(nω0t)}
n=1
に展開できる時、上式各項の係数a0,an,bnをフーリエ係数と呼ぶ。ここで、t;時間、n;波数、ω0;基本振動数(=2π/T)である。
フーリエ係数an,bnは、それぞれ、
T
an=(1/π)∫f(t)cos(nω0t)dt
0
T
bn=(1/π)∫f(t)sin(nω0t)dt
0
として決定できる。
フーリエ係数an,bnは、その係数を用いたフーリエ級数による推定値の残差の自乗の積算
T
∞
∫〔f(t)-a0/2-∑{ancos(nω0t)+bnsin(nω0t)}〕2dt
0
n=1
が最小値を持つan,bnを求めることにより決定できる。上記の式は最大値を持つことはないので、極値を持つとしたら最小値しかない。従って、上式が極値を持つan,bnにおいて上式は最小値を持つ。上式がan,bnにおいて極値を持つ必要十分条件はan,bnにおける上式の偏導関数がセロである。即ち、
T
∞
∂/∂an[∫〔f(t)-a0/2-∑{ancos(nω0t)+bnsin(nω0t)}〕2dt]=0
0
n=1
T
∞
∂/∂bn[∫〔f(t)-a0/2-∑{ancos(nω0t)+bnsin(nω0t)}〕2dt]=0
0
n=1
を満たすan,bnがフーリエ係数である。上式の偏微分を行うと
T
∞
2[∫〔f(t)-a0/2-∑{ancos(nω0t)+bnsin(nω0t)}〕cos(nω0t)dt]=0
0
n=1
T
∞
2[∫〔f(t)-a0/2-∑{ancos(nω0t)+bnsin(nω0t)}〕sin(nω0t)dt]=0
0
n=1
となる。両辺を2で除し、三角関数の直交性を利用して整理すると、上式は、それぞれ、
T
T
∫f(t)cos(nω0t)dt-an∫cos2(nω0t)dt=0
0
0
T
T
∫
f(t)sin(nω0t)dt-an∫sin2(nω0t)dt=0
0
0
となる。
T
T
∫cos2(nω0t)dt=∫sin2(nω0t)dt=π
0
0
だから、これらは、
T
an=(1/π)∫f(t)cos(nω0t)dt
0
T
bn=(1/π)∫f(t)sin(nω0t)dt
0
となり、フーリエ係数を決定できる。
関数f(t)の値が、Δt間隔で離散的に一周期中に等間隔にN個得られている場合には、
Δt=T/N
t=ti=iΔx=Ti/N
とおいて、フーリエ係数の定積分を和分に置き換えると
T
N
an=(1/π)∫f(t)cos(nω0t)dt=(1/π)∑f(ti)cos(2niπ/N)(2π/N)
0
i=1
T
N
bn=(1/π)∫f(t)sin(nω0t)dt=(1/π)∑f(ti)sin(2niπ/N)(2π/N)
0
i=1
であるから、
N
an=(2/N)∑f(ti)cos(2niπ/N)
i=1
N
bn=(2/N)∑f(ti)sin(2niπ/N)
i=1
としてフーリエ係数の値を決定できる。離散化された関数の値が一周期中に等間隔にN個得られている場合、フーリエ係数は第N/2次高調成分までしか決定できない。高調成分の次数を有限で打ち切ったフーリエ級数は、有限フーリエ級数と呼ばれる。
|
フーリエの熱伝導則(Fourier's law of heat conduction)
媒体中のある点における熱フラックス密度は、その点における温度勾配に比例する、とする経験則。熱フラックス密度をQ、熱が流れる方向をx、温度をTとすると、フーリエの熱伝導則は、次式
Q=-k∂T/∂x
により表される。ここで、k;熱伝導率である。熱伝導率は、媒体の密度と比熱と熱拡散率の積に等しい。
|
風速(wind speed, wind velocity)
単位時間当たりの風程をms-1単位で表し、wind
speedと表記したものを風速と言う。この場合はスカラー量であるが、風速と風向を同時に考えたベクトル量をwind
velocityと表記し、これも風速と呼ぶ場合が多い。
|
風程(wind
run)
ある地点を通過した空気塊の一定時間内の移動距離。m単位で表した風程を秒単位であらわした風程を観測時間で割れば風速の値がms-1単位で得られる。
|
風力階級(wind force scale)
Sir Francis Beaufort(1806)により開発された測器に依らない風速の評価体系をビューフォード風力階級と呼ぶ。当初は水夫のために開発されたが、その後陸上での利用のために修正が施された。わが国では、気象業務法施行令(昭和27年政令第471号)第2条第2項の規定に基き、昭和28年運輸省告示第58号により、気象庁風力階級表(ビユーフオート風力階級表)を次のように定めている。名称以外は全て同告示により、英語名はWMO
descriptionを記載し、和名はよく見かけるものを記載した。
気象庁風力階級表(ビユーフオート風力階級表)
|
風力階級
|
開けた平らな地面から10mの高さにおける相当風速
|
名称
|
説明
|
おおよその波高
|
|
|
knot
|
m/s
|
和名
|
英語名
|
陸上
|
海上
|
m
|
feet
|
|
0
|
1未満
|
0.0以上0.3未満
|
静穏
|
Calm
|
静穏 煙はまつすぐに昇る。
|
鏡のような海面
|
―
|
―
|
|
1
|
1以上4未満
|
0.3以上1.6未満
|
至軽風
|
Light Air
|
風向は、煙がなびくのでわかるが風見には感じない。
|
うろこのようなさゞなみができるが、波がしらにあわはない。
|
0.1(0.1)
|
1/4(1/4)
|
|
2
|
4以上7未満
|
1.6以上3.4未満
|
軽風
|
Light Breeze
|
顔に風を感じる。木の葉が動く。風見も動きだす。
|
小波の小さいもので、まだ短いがはつきりしてくる。波がしらはなめらかに見え、砕けていない。
|
0.2(0.3)
|
1/2(1)
|
|
3
|
7以上11未満
|
3.4以上5.5未満
|
軟風
|
Gentle Breeze
|
木の葉や細い小枝がたえず動く。軽い旗が開く。
|
小波の大きいもの。波がしらが砕けはじめる。あわはガラスのように見える。ところどころ白波が現われることがある。
|
0.6(1)
|
2(3)
|
|
4
|
11以上17未満
|
5.5以上8.0未満
|
和風
|
Moderate Breeze
|
砂ほこりが立ち、紙片が舞い上る。小枝が動く。
|
波の小さいもので、長くなる。白波がかなり多くなる。
|
1(1.5)
|
7/2(5)
|
|
5
|
17以上22未満
|
8.0以上10.8未満
|
疾風
|
Fresh Breeze
|
葉のあるかん木がゆれはじめる。池や沼の水面に波がしらが立つ。
|
波の中ぐらいのもので、いつそうはつきりして長くなる。白波がたくさん現われる。(しぶきを生ずることもある。)
|
2(2.5)
|
6(17/2)
|
|
6
|
22以上28未満
|
10.8以上13.9未満
|
雄風
|
Strong Breeze
|
大枝が動く。電線がなる。かさは、さしにくい。
|
波の大きいものができはじめる。いたるところで白くあわだつた波がしらの範囲がいつそう広くなる。(しぶきを生ずることが多い。)
|
3(4)
|
19/2(13)
|
|
7
|
28以上34未満
|
13.9以上17.2未満
|
強風
|
Near Gale
or
Moderate Gale
|
樹木全体がゆれる。風に向つては歩きにくい。
|
波はますます大きくなり、波がしらが砕けてできた白いあわは、すじをひいて風下に吹き流されはじめる。
|
4(5.5)
|
27/2(19)
|
|
8
|
34以上41未満
|
17.2以上20.8未満
|
疾強風
|
Fresh
Gale
or
Gale
|
小枝が折れる。風に向つては歩けない。
|
大波のやや小さいもので長さが長くなる。波がしらの端は砕けて水けむりとなりはじめる。あわは明りようなすじをひいて風下に吹き流される。
|
5.5(7.5)
|
36(25)
|
|
9
|
41以上48未満
|
20.8以上24.5未満
|
大強風
|
Strong Gale
|
人家にわずかの損害がおこる。(煙突が倒れ、かわらがはがれる。)
|
大波。あわは濃いすじをひいて風下に吹き流される。波がしらはのめり、くずれ落ち、逆巻きはじめる。しぶきのため視程がそこなわれることもある。
|
7(10)
|
23(32)
|
|
10
|
48以上56未満
|
24.5以上28.5未満
|
全強風
|
Whole
Gale
or
Storm
|
陸地の内部ではめずらしい。樹木が根こそぎになる。人家に大損害がおこる。
|
波がしらが長くのしかかるような非常に高い大波。大きなかたまりとなつたあわは濃い白色のすじをひいて風下に吹き流される。海面は全体として白く見える。波のくずれかたは、はげしく衝撃的になる。視程はそこなわれる。
|
9(12.5)
|
29(41)
|
|
11
|
56以上64未満
|
28.5以上32.7未満
|
暴風
|
Violent Storm
|
めつたにおこらない。広い範囲の破壊を伴う。
|
山のように高い大波(中小船舶は、一時波の陰にみえなくなることもある。)。海面は、風下に吹き流された長い白色のあわのかたまりで完全におおわれる。いたるところで波がしらの端が吹きとばされて水けむりとなる。視程はそこなわれる。
|
11.5(16)
|
37(52)
|
|
12
|
64以上
|
32.7以上
|
颱風
|
Hurricane
|
―
|
大気は泡としぶきが充満する。海面は吹きとぶしぶきのために完全に白くなる。視程は著しくそこなわれる。
|
14(―)
|
45(―)
|
|
副尺(vernier)
いろいろな装置の読み取り目盛り(主尺)の最小目盛りよりも小さい値まで正確に読み取れるように工夫された補助目盛り。発明者の名前に基づく呼称。副尺は主尺の最小目盛り(n-1)目盛りをn等分した目盛りを持つ。読み取らねばならない値は副尺の目盛りの0が示す主尺の目盛りの値であるが、当然のことながら、当該の場所には主尺には目盛りは存在しないので、主尺だけの場合には、最小目盛りより下の桁の数値は目分量で読むほかない。副尺を利用すると、最小目盛りのn分の1の目盛りの値まで正確に決定できる。
例えば、主尺の目盛りのlとl+1の間に副尺の目盛り0が位置しており、副尺の目盛り0の位置の主尺の値が
l+x/n
と表される場合を考える。副尺の目盛り間隔が
(n-1)/n
なので、副尺のm番目の目盛りの位置を主尺の目盛りで示すと、
l+x/n+m(n-1)/n
となる。従って、この副尺のm番目の目盛りが、主尺の目盛り(l+m)と完全に一致している場合は、
l+x/n+m(n-1)/n=l+m
が成り立つ。両辺にnをかけると、
ln+x+m(n-1)=ln+mn
なので、両辺からさらに ln+mn を除すると
x=m
が導かれる。すなわち、
l+x/n
のxは、主尺と副尺の目盛りが完全に一致している時の副尺の目盛りmと等しいので、求める主尺の値は
l+m/n
となる。主尺と副尺の目盛りが完全に一致していない場合には、両方の目盛りが最も接近している副尺の目盛りmを探す。副尺の目盛りを多くすればするほど、主尺の目盛りと副尺の目盛りが完全に一致する確率は多くなり高精度の測定が可能となるが、目盛りが一致しているか否かを判断する対象が多数になるため迅速な判断が困難になる。副尺をもつ多くの測定器において、副尺は主尺の9目盛り乃至は19目盛りを10分割乃至は20分割した目盛りを用い、主目盛りの10分の1乃至は20分の1まで読み取れるようになっている。
|
複素相関係数(complex
correlation coefficient)
一組の複素数の数列x(t)とy(t)の間の相関関係の程度を測る指標として、次のように定義される複素相関係数κxyが用いられる。
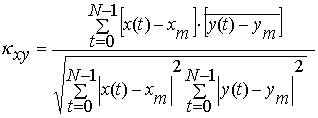
ここで、N:データの数、xm:x(t)の平均値、ym:y(t)の平均値、 :複素共役である。当然のことながら複素相関係数κxyは複素数である。
|
ブジネスク近似(Boussinesq
approximation)
空間的な温度差が小さく、従って、空間的な密度差も小さいが、浮力による流れは駆動されている流体の支配則において、重力加速度gが掛かっている項(浮力項)以外における密度差を無視する近似をブジネスク近似と呼ぶ。ブジネスク近似が成り立つ流れはブジネスク流と呼ばれることがある。
|
フェレルの法則(Ferrel's law)
北半球においては風は右方向に進路がずれ、南半球では左にずれるという法則。気塊の運動にコリオリの効果をあてはめて導くことができる。
|
沸点(boiling point)
液体が、標準気圧(=1013.245hPa)の大気圧下において沸騰する温度。水の沸点は100℃(=373.15K)である。
|
沸騰(boiling)
液体の中に蒸気のみからなる気泡が発生した時、蒸気圧が大気圧以下であれば大気圧に押しつぶされて蒸気のみからなる気泡はつぶれるが、蒸気圧が大気圧以上になると蒸気のみからなる気泡は大気圧に打ち勝って大きくなり、周りの液体から蒸発する蒸気を取り込んでどんどん大きくなっていく。この現象を沸騰という。沸騰は飽和蒸気圧が大気圧と等しい時に発生する。飽和蒸気圧は温度に依存するので、大気圧が大きいほど、沸騰が発生する温度は高くなる。通常の蒸発では液体の表面からのみ蒸気が発生するのに対して、沸騰では液体の内部全域から蒸気が発生する。
|
フットプリント(footprint)
もともとは機器の底面や機器を設置するのに必要な面積を指す言葉だが、衛星リモートセンシングの分野では、衛星がデータを取得している地域をフットプリントと呼び、航跡という邦語訳を与えている。気象学では、観測機器により得られる値が得られる空間を当該測器のフットプリントと呼ぶことがある。微気象における 地表面熱収支インバランス問題の原因として、各測器の精度とともに各測器ごとにフットプリントが異なることが指摘されている。
|
普遍気体定数(universal gas constant)
気体の圧力p(Pa)と体積V(m3)の積がモル数n/mと温度T(K)の積に比例する時の比例定数を普遍気体定数と呼び、R*と表記する。即ち、
pV=(n/m)R*T
が成り立ち、理想気体の状態方程式と呼ばれ、これらのパラメータが上記の式を満たす気体を理想気体と呼ぶ。ここで、n;気体の質量、m;気体の分子量である。普遍気体定数R*の値は気体の種類によらず一定であり、8314.51JK-1であることが知られている。
|
フラックス(flux)
考察の対象にしている面を垂直に横切る物理量の輸送速度をフラックスと呼ぶが、しばしば色々な形態のエネルギー輸送に対して用いられる。気象学の分野では、しばしば、フラックス密度の短縮形としてフラックスという用語が用いられる。
|
フラックス密度(flux density)
考察の対象にしている面の単位面積を垂直に横切る物理量の輸送速度をフラックスと呼ぶが、しばしば色々な形態のエネルギー輸送に対して用いられる。気象学の分野では、しばしば、フラックス密度の短縮形としてフラックスという用語を用いる。一般的には、物理量θのフラックス密度fは、
f=ρθv
と表現される。ここで、ρ;密度、θ;単位質量当りの物理量、v;物質の速度である。例えば、物理量θとして顕熱CpTや潜熱ℓqを用いると顕熱フラックス密度はがρCpTv、潜熱フラックス密度はρℓqvと表される。ここで、Cp;空気の定圧比熱、T;気温、ℓ;蒸発の潜熱、q;比湿である。
放射の分野では、考察の対象にしている面の単位面積を垂直に横切る放射エネルギーを放射フラックス密度と呼び、Wm-2単位で表される。
|
プラント・バイサラ振動数(Brunt–Väisälä
Frequency, Brunt-Visla
frequency)
安定成層している気層中を空気塊が浮力による復元力を受けて上下に変位する単振動をプラント・バイサラ振動と呼び、その振動数をプラント・バイサラ振動数と呼ぶ。
周囲の気温がTの時、気温T’の単位質量の空気塊に作用する浮力による運動方程式は
d2z/dt2=g(T’-T)/T
と表現される。ここで、t;時間、z;変位、g;重量加速度である。変位する空気塊の気温減率は乾燥断熱減率に等しくてΓd(=g/Cp=0.00976Km-1)であり、周囲の気温減率をΓとすると、変位する空気塊と周囲の大気の気温の鉛直分布は、それぞれ、
T’=T0’-Γdz
T=T0-Γz
と表示できるので、両者の差を取れば、
T’-T=-(Γd-Γ)
となり、上式は、
d2z/dt2=-g(Γd-Γ)z/T
と表記できる。ここで、
N2=g(Γd-Γ)/T
と置けば、上記の運動方程式は、
d2z/dt2=
-N2z
と表記される。これは振動数Nの単振動の式であるので、一般解は、
z=Asin(Nt+φ)
と表せ、空気塊は、振幅A、周期2π/Nで基準高度の周囲を振動する。この振動はブラントバイサラ振動と呼ばれ、Nおよびは2π/Nは、それぞれ、プラント・バイサラ振動の振動数、周期と呼ばれる。
プラント・バイサラ振動数は
N2= g(∂T/∂z+
g/Cp)/T
とも表現でき、これは温位θを用いて表現すると、温位勾配が
∂θ/∂z=θ/T(∂T/∂z+g/Cp)
と表されることから、
N2= (g/θ)∂θ/∂z
とも表現できる。ここで、Cp;定圧比熱である。また、プラント・バイサラ振動数は、
N2= -g∂logeρ/∂z-g2/Cs2
とも表現できる。ここで、ρ;密度、Cs;音速である。即ち、プラント・バイサラ振動数は、温度勾配∂T/∂zや温位勾配∂θ/∂z、密度勾配∂logeρ/∂zで表現することが可能というか、大気の安定度を表す指標の一つ、という位置づけができる。例えば、温位θ=288.15K、温位勾配∂θ/∂z=0.0035Km-1、重力加速度g=9.80665ms-2とすると、プラント・バイサラ振動数Nは0.0109s-1、プラント・バイサラ振動周期2π/Nは575.7s、即ち、9.6minとなる。
|
プランクの関数(Planck function)
単位質量当たり単位波長当たりの黒体から射出される放射エネルギーBλを温度Tおよび波長λの関数と示す式で、以下のように表現される。Bλ=(8πhc/λ5)/(ehc/λkT-1)
ここで、h:プランク定数、c:光速、k:はボルツマン定数である。このため、放射は波長範囲によって、赤外線、可視光線、紫外線、X線などに分類される。プランクの関数を波長λの全域について積分するとステファンボルツマンの法則が得られる。プランクの関数の波長λでの微分が0になる条件を求めるとウィーンの変位則が求まる。
|
浮力(buoyancy)
空気塊は当該空気塊が排除した容積の周辺空気が受ける重力と同じ大きさの浮力を受ける。気象学では、当該空気塊が受ける浮力から当該空気塊が受ける重力を差し引いたいわゆる純浮力を当該空気塊が受ける浮力と呼んでいる。空気塊の内圧、気温をそれぞれp'、T'、周辺空気のとの外圧、気温をそれぞれp、T、とすると、当該空気塊の体積と密度は、状態方程式より、それぞれ、
RT'/p'
p'/RT'
なので、当該空気塊が受ける重力は
p'/RT'×g×RT'/p'
であり、当該空気塊が排除する周辺空気が受ける重力は
p/RT×g×RT'/p'
となり、ここで言う浮力(純浮力)は両者の差
p/RT×g×RT'/p'-p'/RT'×g×RT'/p'={p'/T'-p/T}g/R×RT'/p'
となる。しかるに、内圧と外圧は等しい(p'=p)ので、上式は、
{1/T-1/T'}gT'=g(T'-T)/T
と変形できる。つまり、当該空気塊が受ける浮力は
g(T'-T)/T
と表現できる。
|
|
|
フルード数 (Froude number)
気流の障害物の乗り越え易さを表す指標で、次式
Fr=U/(Nh)
で定義されるパラメータFrをフルード数と呼ぶ。ここで、U;風速、N;ブラントバイサラ振動数、h;山岳等の障害物の高さである。ブラントバイサラ振動数Nの定義式は
N2= (g/θ)∂θ/∂z
なので、風速が大きく、かつ温位勾配と障害物の高さが小さくてフルード数Fr>1の場合、気流は障害物を乗り越え易い。逆に、風速が小さく、かつ温位勾配と障害物の高さが大きくてフルード数Fr<1の場合、気流は障害物を乗り越え難く迂回する 。
開水路の流れの状態を表すためにもフルード数Frが用いられ、その際の定義式は、
Fr=U/(gh)0.5
である。ここで、h;水深、g;重力加速度である。この式の右辺の分母は、深さhの浅水波の進行速度を意味する。即ち、フルード数Frは、流速と波の進行速度の比を表しており、フルード数Fr>1の場合は流速が波の進行速度より大きい射流となり、フルード数Fr<1の場合は流速が波の進行速度より小さい常流となる。
|
分圧(partial
pressure)
混合気体の構成成分気体の圧力。混合気体全体の圧力は全構成成分気体の分圧の総和に等しく、全圧と呼ばれる。例えば、湿潤空気は乾燥空気と水蒸気の混合気体であるので、気圧が全圧であり、乾燥空気圧と水蒸気圧が、それぞれの成分の分圧である。
|
分裂ストーム(splitting
storm)
本来の進行方向から左右にそれた方向へ進む2つの雷雨left
moverとright moverに分裂する雷雨を分裂ストームと呼ぶ。
分裂ストームは、ストームの進行方向とは垂直な方向に水平渦軸を持つ強い水平風鉛直シアが存在する場において雷雲が発達すると出現する。水平な渦線の雷雨の中心と遭遇した部分が雷雨の上昇気流により持上げられることにより渦線の立ち上がりが生じ、上昇気流の中の雷雨の進行方向に垂直な面内に逆Uの字型に折れ曲がった2本の鉛直な渦線が発生する。2本の鉛直な渦線のうち、雷雨進行方向右側の渦線は正の渦度(低気圧性の回転)を持ち、左側の渦線は負の渦度(高気圧性の回転)を持つ。上昇気流による渦線の伸長のためそれぞれの渦度の絶対値が増加する。上昇気流の中心部上層では新たな凝結が発生し新たな降水が発生する。新たな降水が引き起こす下降気流のためそれまでの上昇気流中心部の渦線は下方に折れ曲がる事態となり、雷雨の中心部には雷雨の進行方向に垂直な面内に逆Wの字型に折れ曲がった4本の渦線が形成されるようになる。4本の渦線のうち、外側の2本は中央部の下降気流が発生する以前からと同様に上昇気流の場にあり、雷雨進行方向右側の渦線は正の渦度(低気圧性の回転)を持ち、左側の渦線は負の渦度(高気圧性の回転)を持つ。しかし、内側の2本は下降気流の場にあり、雷雨進行方向右側の渦線は負の渦度(高気圧性の回転)を持ち、左側の渦線は正の渦度(低気圧性の回転)を持つため、この領域では、下降気流が発生する以前の渦度を打ち消す結果となる。このため、雷雨中心部は渦度の絶対値が小さい寒冷な下降する空気塊で占められるようになり、雷雨は進行方向右側の正の渦度(低気圧性の回転)を持つ雷雨right
moverと、進行方向左側の負の渦度(高気圧性の回転)を持つ雷雨left
moverに分裂する。
回転するストームや分裂ストームには水平風鉛直シアの存在が不可欠だが、ストームの回転、分裂以外にも水平風鉛直シアの影響は現れる。水平風鉛直シアが存在すると、同高度の圧力分布に乱れが発生し、水平風鉛直シアベクトルの始点側が高圧になり終点側が低圧になる。このため、地上付近では、水平風鉛直シアベクトルの始点側では上空ほど高圧場になり下降気流が生じるのに対して、終点側では上層ほど低圧場になり上昇気流が生じる。従って、地上付近から上層まで風向が一定で風速のシアだけが存在する場合には、雷雨の上昇気流の中心部を風下側に移動させる効果が生じることになる。しかしながら、実際には、中層においてストームの進行方向の右側から比較的乾燥した空気塊が入ってくることが多く、地上から上層に向かって反時計回りの風向のシアが存在することが多く、この場合は、上昇に行くに従って水平風鉛直シアベクトルの方向が変わるため、上層ほど高圧場になり下降気流が強化されるのは雷雨の進行方向後方ではなくて進行方向左側となり、上層ほど低圧場になり上昇気流が強化されるのは進行方向右側となる。この結果、分裂したストームのうち、進行方向右側の正の渦度(低気圧性の回転)を持つ雷雨right
moverは上昇気流が弱まりやがて消滅する傾向があるのに対して、進行方向左側の負の渦度(高気圧性の回転)を持つ雷雨left
moverは上昇気流がさらに強化されて、いわゆるスーパーセル型ストームに成長する傾向が顕著である。竜巻はスーパーセル型ストームの中で発生しやすいので、竜巻の回転方向は圧倒的に左回りが多い。
|
|
|
|